ARITHMETIC CIRCUITS BASIC BUILDING BLOCKS TUTORIALS

In this article, we will discuss those combinational logic building blocks that can be used to perform addition and subtraction operations on binary numbers. Addition and subtraction are the two most commonly used arithmetic operations, as the other two, namely multiplication and division, are respectively the processes of repeated addition and repeated subtraction

We will begin with the basic building blocks that form the basis of all hardware used to perform the aforesaid arithmetic operations on binary numbers. These include half-adder, full adder, half-subtractor, full subtractor and controlled inverter.


A half-adder is an arithmetic circuit block that can be used to add two bits. Such a circuit thus has two inputs that represent the two bits to be added and two outputs, with one producing the SUM output and the other producing the CARRY.

The Boolean expressions for the SUM and CARRY outputs are given by the equations
SUM S = A B+A B
CARRY C = A B


A full adder circuit is an arithmetic circuit block that can be used to add three bits to produce a SUM and a CARRY output. Such a building block becomes a necessity when it comes to adding binary numbers with a large number of bits.

The full adder circuit overcomes the limitation of the half-adder, which can be used to add two bits only. Let us recall the procedure for adding larger binary numbers. We begin with the addition of LSBs of the two numbers. We record the sum under the LSB column and take the carry, if any, forward to the next higher column bits.


A half-subtractor is a combinational circuit that can be used to subtract one binary digit from another to produce a DIFFERENCE output and a BORROW output. The BORROW output here specifies whether a ‘1’ has been borrowed to perform the subtraction.


A full subtractor performs subtraction operation on two bits, a minuend and a subtrahend, and also takes into consideration whether a ‘1’ has already been borrowed by the previous adjacent lower minuend bit or not.

As a result, there are three bits to be handled at the input of a full subtractor, namely the two bits to be subtracted and a borrow bit designated as Bin . There are two outputs, namely the DIFFERENCE output D and the BORROW output Bo. The BORROW output bit tells whether the minuend bit needs to borrow a ‘1’ from the next possible higher minuend bit.


A controlled inverter is needed when an adder is to be used as a subtractor. As outlined earlier, subtraction is nothing but addition of the 2’s complement of the subtrahend to the minuend. Thus, the first step towards practical implementation of a subtractor is to determine the 2’s complement of the subtrahend. And for this, one needs firstly to find 1’s complement. A controlled inverter is used to find 1’s complement.

LOGIC GATES BASIC INFORMATION AND TUTORIALS

The logic gate is the most basic building block of any digital system, including computers. Each one of the basic logic gates is a piece of hardware or an electronic circuit that can be used to implement some basic logic expression.

While laws of Boolean algebra could be used to do manipulation with binary variables and simplify logic expressions, these are actually implemented in a digital system with the help of electronic circuits called logic gates.

The three basic logic gates are the OR gate, the AND gate and the NOT gate.

OR GATE
An OR gate performs an ORing operation on two or more than two logic variables. The OR operation on two independent logic variables A and B is written as Y = A+B and reads as Y equals A OR B and not as A plus B.

An OR gate is a logic circuit with two or more inputs and one output. The output of an OR gate is LOW only when all of its inputs are LOW. For all other possible input combinations, the output is HIGH. This statement when interpreted for a positive logic system means the following.

The output of an OR gate is a logic ‘0’ only when all of its inputs are at logic ‘0’. For all other possible input combinations, the output is a logic ‘1’. Figure 4.3 shows the circuit symbol and the truth table of a two-input OR gate. The operation of a two-input OR gate is explained by the logic expression Y = A+B


AND GATE
An AND gate is a logic circuit having two or more inputs and one output. The output of an AND gate is HIGH only when all of its inputs are in the HIGH state. In all other cases, the output is LOW.

When interpreted for a positive logic system, this means that the output of the AND gate is a logic ‘1’ only when all of its inputs are in logic ‘1’ state. In all other cases, the output is logic ‘0’.

The AND operation on two independent logic variables A and B is written as Y = A B and reads as Y equals A AND B and not as A multiplied by B. Here, A and B are input logic variables and Y is the output.

NOT GATE
A NOT gate is a one-input, one-output logic circuit whose output is always the complement of the input. That is, a LOW input produces a HIGH output, and vice versa.

When interpreted for a positive logic system, a logic ‘0’ at the input produces a logic ‘1’ at the output, and vice versa. It is also known as a ‘complementing circuit’ or an ‘inverting circuit’.

The NOT operation on a logic variable X is denoted as X or X . That is, if X is the input to a NOT circuit, then its output Y is given by Y = X or X and reads as Y equals NOT X. Thus, if X = 0 Y = 1 and if X = 1 Y = 0.

BINARY SYSTEM BASICS AND TUTORIALS

WHAT IS BINARY NUMBER SYSTEM? A TUTORIAL ON BINARY NUMBER SYSTEM

The binary number system is a radix-2 number system with ‘0’ and ‘1’ as the two independent digits. All larger binary numbers are represented in terms of ‘0’ and ‘1’. The procedure for writing higher order binary numbers after ‘1’ is similar to the one explained in the case of the decimal number system.



For example, the first 16 numbers in the binary number system would be 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110 and 1111. The next number after 1111 is 10000, which is the lowest binary number with five digits.

This also proves the point made earlier that a maximum of only 16 (= 24 numbers could be written with four digits. Starting from the binary point, the place values of different digits in a mixed binary number are 20, 21, 22 and so on (for the integer part) and 2−1, 2−2, 2−3 and so on (for the fractional part).

Example 1.1
Consider an arbitrary number system with the independent digits as 0, 1 and X. What is the radix of this number system? List the first 10 numbers in this number system.

Solution
• The radix of the proposed number system is 3.
• The first 10 numbers in this number system would be 0, 1, X, 10, 11, 1X, X0, X1, XX and 100.

Advantages
Logic operations are the backbone of any digital computer, although solving a problem on computer could involve an arithmetic operation too. The introduction of the mathematics of logic by George Boole laid the foundation for the modern digital computer.

He reduced the mathematics of logic to a binary notation of ‘0’ and ‘1’. As the mathematics of logic was well established and had proved itself to be quite useful in solving all kinds of logical problem, and also as the mathematics of logic (also known as Boolean algebra) had been reduced to a binary notation, the binary number system had a clear edge over other number systems for use in computer systems.

Yet another significant advantage of this number system was that all kinds of data could be conveniently represented in terms of 0s and 1s. Also, basic electronic devices used for hardware implementation could be conveniently and efficiently operated in two distinctly different modes.

For example, a bipolar transistor could be operated either in cut-off or in saturation very efficiently.

Lastly, the circuits required for performing arithmetic operations such as addition, subtraction, multiplication, division, etc., become a simple affair when the data involved are represented in the form of 0s and 1s.

BOOLEAN LOGIC ALGEBRA AND LOGIC GATES BASICS AND TUTORIAL

BOOLEAN LOGIC AND LOGIC GATES TUTORIALS

Machines of all types, including computers, are designed to perform specific tasks in exact well defined manners. Some machine components are purely physical in nature, because their composition and behavior are strictly regulated by chemical, thermodynamic, and physical properties.

For example, an engine is designed to transform the energy released by the combustion of gasoline and oxygen into rotating a crankshaft. Other machine components are algorithmic in nature, because their designs primarily follow constraints necessary to implement a set of logical functions as defined by human beings rather than the laws of physics.

A traffic light’s behavior is predominantly defined by human beings rather than by natural physical laws. This book is concerned with the design of digital systems that are suited to the algorithmic requirements of their particular range of applications. Digital logic and arithmetic are critical building blocks in constructing such systems.

An algorithm is a procedure for solving a problem through a series of finite and specific steps. It can be represented as a set of mathematical formulas, lists of sequential operations, or any combination thereof. Each of these finite steps can be represented by a Boolean logic equation.

Boolean logic is a branch of mathematics that was discovered in the nineteenth century by an English mathematician named George Boole. The basic theory is that logical relationships can be modeled by algebraic equations.

Rather than using arithmetic operations such as addition and subtraction, Boolean algebra employs logical operations including AND, OR, and NOT. Boolean variables have two enumerated values: true and false, represented numerically as 1 and 0, respectively.  The AND operation is mathematically defined as the product of two Boolean values, denoted A and B for reference.

Truth tables are often used to illustrate logical relationships as shown for the AND operation in Table 1.1. A truth table provides a direct mapping between the possible inputs and outputs.

A basic AND operation has two inputs with four possible combinations, because each input can be either 1 or 0 — true or false. Mathematical rules apply to Boolean algebra, resulting in a nonzero product only when both inputs are 1.


Summation is represented by the OR operation in Boolean algebra as shown in Table 1.2. Only one combination of inputs to the OR operation result in a zero sum: 0 + 0 = 0.

Boolean variables may not seem too interesting on their own. It is what they can be made to represent that leads to useful constructs. A rather contrived example can be made from the following logical statement:

“If today is Saturday or Sunday and it is warm, then put on shorts.”

Three Boolean inputs can be inferred from this statement: Saturday, Sunday, and warm. One Boolean output can be inferred: shorts. These four variables can be assembled into a single logic equation that computes the desired result, shorts = (Saturday OR Sunday) AND warm

While this is a simple example, it is representative of the fact that any logical relationship can be expressed algebraically with products and sums by combining the basic logic functions AND, OR, and NOT.

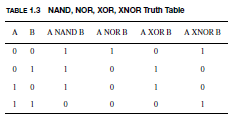
Several other logic functions are regarded as elemental, even though they can be broken down into AND, OR, and NOT functions. These are not–AND (NAND), not–OR (NOR), exclusive–OR (XOR), and exclusive–NOR (XNOR).

Table 1.3 presents the logical definitions of these other basic functions. XOR is an interesting function, because it implements a sum that is distinct from OR by taking into account that 1 + 1 does not equal 1. As will be seen later, XOR plays a key role in arithmetic for this reason.

All binary operators can be chained together to implement a wide function of any number of inputs. For example, the truth table for a ten-input AND function would result in a 1 output only when all inputs are 1.

Similarly, the truth table for a seven-input OR function would result in a 1 output if any of the seven inputs are 1. A four-input XOR, however, will only result in a 1 output if there are an odd number of ones at the inputs.

This is because of the logical daisy chaining of multiple binary XOR operations. As shown in Table 1.3, an even number of 1s presented to an XOR function cancel each other out.

It quickly grows unwieldy to write out the names of logical operators. Concise algebraic expressions are written by using the graphical representations shown in Table 1.4.

Note that each operation has multiple symbolic representations. The choice of representation is a matter of style when handwritten and is predetermined when programming a computer by the syntactical requirements of each computer programming language.

A common means of representing the output of a generic logical function is with the variable Y. Therefore, the AND function of two variables, A and B, can be written as Y = A & B or Y = A*B.

As with normal mathematical notation, products can also be written by placing terms right next to each other, such as Y = AB. Notation for the inverted functions, NAND, NOR, and XNOR, is achieved by inverting the base function.

Two equally valid ways of representing NAND are Y = A & B and Y = !(AB). Similarly, an XNOR might be written as Y = BAR A⊕BAR B.


When logical functions are converted into circuits, graphical representations of the seven basic operators are commonly used. In circuit terminology, the logical operators are called gates . Figure 1.1 shows how the basic logic gates are drawn on a circuit diagram.

Naming the inputs of each gate A and B and the output Y is for reference only; any name can be chosen for convenience. A small bubble is drawn at a gate’s output to indicate a logical inversion.

More complex Boolean functions are created by combining Boolean operators in the same way that arithmetic operators are combined in normal mathematics. Parentheses are useful to explicitly convey precedence information so that there is no ambiguity over how two variables should be
treated.

A Boolean function might be written as Y = (AB + C + )D& BAR E ⊕ BAR F


This same equation could be represented graphically in a circuit diagram, also called a schematic diagram , as shown in Fig. 1.2. This representation uses only two-input logic gates. As already mentioned, binary operators can be chained together to implement functions of more than two variables.

An alternative graphical representation would use a three-input OR gate by collapsing the two-input OR gates into a single entity.