ELECTRONIC PROJECTS | GADGETS NEWS | LATEST TECHNOLOGY | CONSUMER ELECTRONICS
CMOS GATES BASIC AND TUTORIALS
WHAT ARE CMOS GATES? HOW CMOS GATES WORK?
CMOS gates are based on simple modifications to the CMOS inverter.
Figure 8.18(a) and Figure 8.18(b) show that the CMOS NOR and NAND gates are essentially CMOS inverters in which the load and driving transistor are replaced by series or parallel combinations (as appropriate) of PMOS andNMOStransistors, respectively.
Suppose the NOR gate of Fig. 8.18(a) is to have the same VDD and Vinv as the CMOS inverter of Fig. 8.17(a), then the equivalent Zpu and Zpd for the NOR gate should equal those for the inverter.
Since only one of the parallel pull-down transistors needs be on in the NOR to ensure VO = 0V, ZI = Zpd = 1/2 , as for the inverter. For the series load, however, ZL = 1/10 to give equivalent Zpu = 1/5 .
If the NAND gate of Fig. 8.18(b) is to have the same Vinv as the said inverter, similar arguments lead to ZI = 1/4 and ZL = 1/5 for the NAND.
Thus, KR = 0.4 for the inverter, 0.2 for the NOR, and 0.8 (closer to unity) for NAND. Hence, NAND is the standard gate in CMOS.
Another way of putting this is that for the given Z values, if the channel length L is constant, then the widths of the loads for the inverter, NOR, and NAND are in the ratio 1:2:1.
Thus, the NOR requires more chip area, and this larger area requirement increases with the number of inputs.
CMOS INVERTERS BASIC AND TUTORIALS
WHAT ARE CMOS INVERTERS? APPLICATION OF CMOS INVERTERS
As shown in Fig. 8.17(a), the CMOS inverter consists of an enhancement NMOS as the driving transistor, and a complementary enhancement PMOS load transistor. The driving transistor is off when Vin is low, and the load transistor is off when Vin is high.
Thus, one of the two series transistors is always off (equivalently, drain current and power dissipation are zero) except during switching,when both transistors are momentarily on. The resulting low-power dissipation is an important CMOS advantage and makes it an attractive alternative in VLSI design.
NMOS circuits are ratioed in the sense that the pull up never turns off, and VOL is determined by the inverter ratio. CMOS is ratioless in this sense, since VOL is always the negative rail. If one desires equal sourcing and sinking currents, however, the pull-up device must be wider than the pull-down device by the ratio of the electron-to-hole mobilities, typically about 2.5 to 1.
This also gives a symmetrical voltage transfer curve, with the voltage at which Vin = VO having a value of VDD/2. This voltage is referred to as the inverter voltage Vinv.
The voltage transfer for the CMOS inverter is shown in Fig. 8.17(b). Note that the voltage transfer characteristic approaches that of the ideal logic inverter. These characteristics are best obtained with computer circuit simulation programs.
As with the depletion load NMOS inverter, useful insights may be gained by performing an analytical solution. The analysis proceeds as previously described for the depletion load NMOS inverter.
Note that the VTC of Fig. 8.17(b) has been divided into regions as in Fig. 8.15(a). In each region, the appropriate expressions for the load and driving transistor drain currents are equated so that VO can be computed for any given Vin.
To find VI L and VI H, the condition that dVO/dVin = −1 at such critical voltages is applied to the drain current equation.Note that the drain current equations for the PMOS are the same as for NMOS, except for reverse voltage polarities for the PMOS.
PIEZOELECTRIC EFFECT DEFINITION BASIC AND TUTORIALS
WHAT IS PIEZOELECTRIC EFFECT?
Basic Physical Principles
Materials that are used for crystal oscillator applications exhibit the piezoelectric effect. This phenomenon produces an electric field within a material when a mechanical force is applied.
Conversely, if an electrical drive signal is applied to the crystal, a mechanical vibration results. If the driving signal is periodic in nature, then the resulting vibration will also be periodic. Very accurate electric signal frequencies can be produced by certain materialswith the appropriate shape, electrode geometry, and ambient conditions.
For this reason, crystal resonators are used in applications such as television, cellular radio communications, and electronic test equipment where accurate synthesis of signal frequencies is required throughout.
The relationship between the electric field, electric displacement, electric polarization, and mechanical stress and strain is given by what are called constituitive relations. The electrical quantities are related in the following manner:
D = e0 E + P
where D is the electrical displacement, E is the electric field and P is the electric polarization. The term e 0 is the free-space permittivity. The polarization depends on the applied electric field. In a piezoelectric material an electric polarization can also result from an applied stress or strain.
This is called the direct piezoelectric effect. Therefore the polarization is proportional to the stress (T) or strain (S) that is P = dT or P = eS
In the converse piezoelectric effect, the stress or strain forces are generated by the electric field applied to the crystal. Thus, we have S = dE or T = eE
The constants of proportionality d and e are called piezoelectric stress and strain coefficients. The stress and strain forces are represented by matrix quantities, and the coefficients are tensor quantities. A tensor mathematically represents the fact that the polarization can depend on the stress or strain in more than one direction.
This is also true for the relationship between the stress or strain and the electric field. Many other physical properties in crystals also exhibit this nature, which is called anisotropy. Thus when a property is anisotropic, its value depends on the direction of orientation in the crystal.
For the direct piezoelectric effect, the total polarization effect is the sum of these two contributions, an applied electric field and applied mechanical force.
Based on the relationship between the electric displacement and the electric polarization it is then possible to write equations that relate the displacement D to the applied stress or strain. Electric displacement is the quantity that is preferred in experiment and engineering.
SEMICONDUCTORS DEFINITION BASICS AND TUTORIALS
WHAT IS A SEMICONDUCTOR? INFORMATION ABOUT SEMICONDUCTORS
Semiconductors are a categoryofmaterialswith an electrical conductivity that is between that of conductors and insulators. Good conductors, which are all metals, have electrical resistivities down in the range of 10^−6 OHM -cm.
Insulators have electrical resistivities that are up in the range from 10^6 to as much as about 10^12 OHM - cm. Semiconductors have resistivities that are generally in the range of 10^−4–10^4 OHM -cm.
The resistivity of a semiconductor is strongly influenced by impurities, called dopants, that are purposely added to the material to change the electronic characteristics.
We will first consider the case of the pure, or intrinsic semiconductor. As a result of the thermal energy present in the material, electrons can break loose from covalent bonds and become free electrons able to move through the solid and contribute to the electrical conductivity.
The covalent bonds left behind have an electron vacancy called a hole. Electrons from neighboring covalent bonds can easily move into an adjacent bond with an electron vacancy, or hole, and thus the hold can move from one covalent bond to an adjacent bond.
As this process continues, we can say that the hole is moving through the material. These holes act as if they have a positive charge equal in magnitude to the electron charge, and they can also contribute to the electrical conductivity.
Thus, in a semiconductor there are two types of mobile electrical charge carriers that can contribute to the electrical conductivity, the free electrons and the holes. Since the electrons and holes are generated in equal numbers, and recombine in equal numbers, the free electron and hole populations are equal.
In the extrinsic or doped semiconductor, impurities are purposely added to modify the electronic characteristics. In the case of silicon, every silicon atom shares its four valence electrons with each of its four nearest neighbors in covalent bonds.
If an impurity or dopant atom with a valency of five, such as phosphorus, is substituted for silicon, four of the five valence electrons of the dopant atom will be held in covalent bonds. The extra, or fifth electron will not be in a covalent bond, and is loosely held.
At room temperature, almost all of these extra electronswill have broken loose fromtheir parent atoms, and become free electrons. These pentavalent dopants thus donate free electrons to the semiconductor and are called donors.
These donated electrons upset the balance between the electron and hole populations, so there are now more electrons than holes. This is now called an N-type semiconductor, in which the electrons are the majority carriers, and holes are the minority carriers.
In an N-type semiconductor the free electron concentration is generally many orders of magnitude larger than the hole concentration. If an impurity or dopant atom with a valency of three, such as boron, is substituted for silicon, three of the four valence electrons of the dopant atom will be held in covalent bonds.
One of the covalent bonds will be missing an electron. An electron from a neighboring silicon-to-silicon covalent bond, however, can easily jump into this electron vacancy, thereby creating a vacancy, or hole, in the silicon-to-silicon covalent bond. Thus, these trivalent dopants accept free electrons, thereby generating holes, and are called acceptors.
These additional holes upset the balance between the electron and hole populations, and so there are now more holes than electrons. This is called a P-type semiconductor, in which the holes are the majority carriers, and the electrons are the minority carriers. In a P-type semiconductor the hole concentration is generally many orders of magnitude larger than the electron concentration.
The transition between the two sides is called the PN junction. As a result of the concentration difference of the free electrons and holes there will be an initial flow of these charge carriers across the junction, which will result in the N-type side attaining a net positive charge with respect to the P-type side.
This results in the formation of an electric potential hill or barrier at the junction. Under equilibrium conditions the height of this potential hill, called the contact potential is such that the flow of the majority carrier holes from the P-type side up the hill to the N-type side is reduced to the extent that it becomes equal to the flow of the minority carrier holes from the N-type side down the hill to the P-type side.
Similarly, the flow of the majority carrier free electrons fromthe N-type side is reduced to the extent that it becomes equal to the flow of the minority carrier electrons from the P-type side. Thus, the net current flow across the junction under equilibrium conditions is zero.
RADAR - RADIO DETECTION AND RANGING APPLICATIONS BASIC AND TUTORIALS
WHAT ARE THE APPLICATIONS OF RADAR - RADIO DETECTION AND RANGING
Radars can be classified by frequency band, use, or platform, for example, ground based, shipborne, airborne, or spaceborne. Radars generally operate in the microwave regime although HF over-the-horizon (OTH) radars such as JINDALEE, OTHB, and ROTHR use similar principles in bouncing signals from the ionosphere to achieve long-range coverage.
Radars are often denoted by the letter band of operation, for example, L-band (1–2 GHz), S-band (2–4 GHz), C-band (4–8 GHz), and X-band (8–12 GHz). Some classifications of radar are based on propagation mode (e.g., monostatic, bistatic, OTH, underground) or on scan method (mechanical, electronic, multibeam).
Other classifications of radar are based on the waveform and processing, for example, pulse Doppler (PD), continuous wave (CW), FM/CW, synthetic aperture radar (SAR) or impulse (wideband video).
Radars are often classified by their use: weather radar, police speed detection, navigation, precision approach radar, airport surveillance and air route surveillance, radio astronomy, fire control and weapon direction, terrain mapping and avoidance, missile fuzing, missile seeker, foliage penetration, subsurface or ground penetrating, acquisition, orbital debris, range instrumentation, imaging (e.g., SAR/ISAR), etc.
Search (or surveillance) radars are concerned with detection of targets out to long range and lowelevation angles to allow adequate warning on pop-up low-flying targets (e.g., sea skimmers). Since the search radar is more concerned with detection (i.e., presence or absence of targets) and can accommodate cruder accuracy in estimating target parameters such as azimuth angle, elevation angle, and range, search radars tend to have poorer range and angle accuracy than tracking radars.
The frequency tends to be lower than track radars since RF power and antenna aperture are less expensive and frequency stability is better. Broad beams (e.g., fan beam) allow faster search of the volume. To first order, the radar search performance is driven by the power-aperture product (PA) to search the volume with a given probability of detection (PD) in a specified frame time.
PA actually varies slightly in that to maintain a fixed false alarm rate per scan, more beam positions offer more opportunities for false alarms and, hence, the detection threshold must be raised, which increases the power to achieve the specified PD.With a phased-array antenna (i.e., electronically scanned beam), the probability of false alarm can be optimized by setting a high false alarm in the search beam and using a verify beam with higher threshold to confirm whether a search detection was an actual target or just a false alarm.
The lower threshold in search allows less search power with some fraction of beams requiring the extra verify beams. The net effect on total required transmit power can be a reduction using this optimization technique.
Search radars tend to use a fan beam or stacked receive beams to reduce the number of beam positions allowing more time in the beam for coherent processing to reduce clutter. Fill pulses are sometimes used to allow good clutter cancellation on second- or higher time-around clutter returns.
Track radars tend to operate at higher frequency and have better accuracy, that is, narrower beams and high range resolution. Simple radars track a single target with an early–late range tracker, Doppler speed gate, and conical scan or sequential lobing.
More advanced angle trackers use monopulse or conical scan on receive only (COSRO) to deny inverse modulation by repeater jammers. The multifunction phased-array radar can be programmed to conduct searches with track beams assigned to individual detected targets.
The tracks are maintained in track files. If time occupancy becomes a problem, the track pulses can be machine gunned out at the targets in range order, and on receive they are gathered in one after the other since the track window on each target is quite small. In mechanically rotated systems, track is often a part of search, for example, track-while-scan (TWS).
A plot extractor clusters the primitive returns in range Doppler angle from a given target to produce a single plot. The plots are associated with the track files using scan-to-scan correlation gates. The number of targets that can be handled in a TWS system is limited by data processing rather than track power.
ANTENNA BANDWIDTH BASIC AND TUTORIALS
WHAT IS ANTENNA BANDWIDTH? THE PURPOSE OF ANTENNA BANDWIDTH?
Antennas can find use in systems that require narrow or large bandwidths depending on the intended application. Bandwidth is a measure of the frequency range over which a parameter, such as impedance, remains within a given tolerance. Dipoles, for example, by their nature are very narrow band.
For narrow-band antennas, the percent bandwidth can be written as:
(fu - fl)/fc x 100
where
fL = lowest useable frequency
fU = highest useable frequency
fC = center design frequency
In the case of a broadband antenna it is more convenient to express bandwidth as
fU/fL
One can arbitrarily define an antenna to be broadband if the impedance, for instance, does not change
significantly over one octave ( fU / fL = 2).
The design of a broadband antenna relies in part on the concept of a frequency-independent antenna. This is an idealized concept, but understanding of the theory can lead to practical applications.
Broadband antennas are of the helical, biconical, spiral, and log-periodic types. Frequency independent antenna concepts are discussed later in this chapter.
Some newer concepts employing the idea of fractals are also discussed for a new class of wideband antennas.
Narrow-band antennas can be made to operate over several frequency bands by adding resonant circuits in series with the antenna wire. Such traps allow a dipole to be used at several spot frequencies, but the dipole still has a narrow band around the central operating frequency in each band.
Another technique for increasing the bandwidth of narrow-band antennas is to add parasitic elements, such as is done in the case of the open-sleeve antenna (Hall, 1992).
COMMON COLLECTOR TRANSISTOR CONFIGURATION BASICS AND TUTORIALS
WHAT IS COMMON COLLECTOR TRANSISTOR CONFIGURATION
Figure 1 is a practical example of a common-collector transistor amplifier. Note that the output is taken off of the emitter instead of the collector (as in the common-emitter configuration).
A common-collector amplifier is not capable of voltage gain. In fact, there is a very slight loss of voltage amplitude between input and output.
 | ||||||||
Essentially, the output signal is an exact duplicate of the input signal. For this reason, common-collector amplifiers are often called emitter-follower amplifiers, because the emitter voltage follows the base voltage.
Common-collector amplifiers are current amplifiers. The current gain for the circuit illustrated in Fig. 1 is the parallel resistance value of R1 and R2, divided by the resistance value of R3. R1 and R2 are both 20 Kohms in value, so their parallel resistance value is 10 Kohms.
This 10 Kohms divided by 1 Kohm (the value of R3) gives us a current gain of 10 for this circuit. Because the voltage gain is considered to be unity (1), the power gain for a common-collector amplifier is considered equal to the current gain (10, in this particular case).
The input impedance of common-collector amplifiers is typically higher than the other transistor configurations. It is the parallel resistive effect of R1, R2, and the product of the value of R3 times the beta value.
Because beta times the R3 value is usually much higher than that of R1 or R2, you can closely estimate the input impedance by simply considering it to be the parallel resistance of R1 and R2. In this case, the input impedance would be about 10 Kohms.
The traditional method of calculating the output impedance of common-collector amplifiers is to divide the value of R3 by the transistor’s beta value. Although this method is still appropriate, a closer estimate can probably be obtained by considering the output impedance of most transistors to be about 80 ohms.
This 80-ohm output impedance should be viewed as being in parallel with R3, giving us a calculated output impedance of about 74 ohms (80 ohms in parallel with 1000 ohms). Resistors R1 and R2 have the same function within a common-collector amplifier as previously discussed with common-emitter amplifiers.
The high negative feedback produced by R3 provides excellent temperature stability and immunity from transistor variables. The circuit illustrated in Fig. 1 can be a valuable building block toward future projects.
HISTORY OF SOLID STATE ELECTRONICS BASICS
SOLID STATE ELECTRONICS BRIEF HISTORY
The crystal detectors used in early radios were the forerunners of modern solid-state devices. However, the era of solid-state electronics began with the invention of the transistor in 1947 at Bell Labs.
The inventors were Walter Brattain, John Bardeen, and William Shockley. PC (printed circuit) boards were introduced in 1947, the year the transistor was invented. Commercial manufacturing of transistors began in Allentown, Pennsylvania, in 1951.
The most important invention of the 1950s was the integrated circuit. On September 12, 1958, Jack Kilby, at Texas Instruments, made the first integrated circuit. This invention literally created the modern computer age and brought about sweeping changes in medicine, communication, manufacturing, and the entertainment industry.
Many billions of "chips"-as integrated circuits came to be called-have since been manufactured. The 1960s saw the space race begin and spurred work on miniaturization and computers.
The space race was the driving force behind the rapid changes in electronics that followed. The first successful "op-amp" was designed by Bob Widlar at Fairchild Semiconductor in 1965. Called the flA709, it was very successful but suffered from "latch-up" and other problems.
Later, the most popular op-amp ever, the 741, was taking shape at Fairchild. This opamp became the industry standard and influenced design of op-amps for years to come.
By 1971, a new company that had been formed by a group from Fairchild introduced the first microprocessor. The company was Intel and the product was the 4004 chip, which had the same processing power as the Eniac computer.
Later in the same year, Intel announced the first 8-bit processor, the 8008. In 1975, the first personal computer was introduced by Altair, and Popular Science magazine featured it on the cover of the January, 1975, issue.
The 1970s also saw the introduction of the pocket calculator and new developments in optical integrated circuits.
By the 1980s, half of all U.S. homes were using cable hookups instead of television antennas. The reliability, speed, and miniaturization of electronics continued throughout the 1980s, including automated testing and calibrating of PC boards. The computer became a part of instrumentation and the virtual instrument was created. Computers became a standard tool on the workbench.
The 1990s saw a widespread application of the Internet. In 1993, there were 130 websites, and now there are millions. Companies scrambled to establish a home page and many of the early developments of radio broadcasting had parallels with the Internet.
In 1995, the FCC allocated spectrum space for a new service called Digital Audio Radio Service. Digital television standards were adopted in 1996 by the FCC for the nation's next generation of broadcast television.
The 21st century dawned in January 2001. One of the major technology stories has been the continuous and explosive growth of the Internet. Internet usage in North America has increased by over 100% from 2000 to 2005.
The rest of the world experienced almost 200% growth during the same period. The processing speed of computers is increasing at a steady rate and data storage media capacity is increasing at an amazing pace. Carbon nanotubes are seen to be the next step forward for computer chips, eventually replacing transistor technology.
BREADBOARD AND PRINTED CIRCUIT BOARD BASICS AND TUTORIALS
WHAT ARE BREADBOARD AND PRINTED CIRCUIT BOARD?
A breadboard is a rectangular plastic box filled with holes, which have contacts in which you can insert electronic components and wires. A breadboard is what you use to string together a temporary version of your circuit.
You don’t have to solder wires or anything else; instead, you poke your components and wires into the little contact holes arranged in rows and connected by lines of metal; then you can connect your components together with wires to form your circuit.
The nice thing about breadboards is that you can change your mind and replace or rearrange components as you like. You typically create an electronics project on a breadboard to make sure that everything works.
If it’s a project you wish to save, you can create a more permanent version. If you want to create a permanent version of your circuit, you need to create a soldered or printed circuit board; see the sidebar, “Printed circuit boards,” to find out how to go about that.
Printed circuit boards
If you create a circuit on a breadboard and decide that it’s worthy of immortality, you can make it permanent by soldering components in place on a printed circuit board. To do this, you have to get your hands on a universal printed circuit board.
This is much like a breadboard except that you can solder all the connections you’ve made to keep them around. A universal printed circuit board has rows of individual holes throughout the board with copper pads around each hole and metal lines connecting the holes in each row, like in a breadboard.
You mount parts on the face of the board and then pass leads through holes to the components. You can solder the leads to the copper pads on the bottom of the board.
Universal printed circuit boards are available in a variety of patterns of contact holes and
metal lines. The figure here shows one we like because there are rows on either side that accommodate discrete components handily.
You can get custom printed circuit boards made for your circuit; this is typically done by submitting a drawing of your circuit to a printed circuit board company. These boards eliminate the need to solder jumper wires between components.
SAFETY USE OF SOLDERING IRON TUTORIALS
SOLDERING SAFETY TIPS
Soldering poses a few different dangers. (You might use solder to attach various pieces of your electronics project, such as soldering wires onto a speaker, microphone, or switch.) The soldering iron itself gets mighty hot.
The solder (the material you heat with the iron) gets hot. Occasionally, you even get an air pocket or impurity in solder that can pop as you heat it, splattering a little solder toward your face or onto your arm.
To top that off, hot solder produces some nasty fumes. Soldering itself takes experience to get right. Your best bet is to have somebody who is good at it teach you.
Here are some soldering safety guidelines you should always follow:
1. Always wear safety glasses when soldering.
2. Never solder a live circuit (one that is energized). Soldering irons come in models that use different wattages. Use the right size soldering iron for your projects; too much heat could ruin your board or components.
3. Solder in a well-ventilated space to prevent the mildly caustic and toxic fumes from building up and causing eye or throat irritation.
4. Always put your soldering iron back in its stand when not in use. Too, be sure that the stand is weighted enough or attached to your worktable so that it doesn’t topple over if you should brush against the cord.
5. NEVER place a hot soldering iron on your work surface. You could start a fire.
6. Give any soldered surface a minute or two to cool down before you touch it.
7. Never, ever try to catch a hot soldering iron if you drop it. No matter how hard you try, you are very likely to grab the hot end in a freefall. Let it fall; buy a new one if you have to — just don’t grab!
8. Never leave flammable items (like paper) near your soldering iron.
9. Be sure to unplug your soldering iron when you’re not around.
Don’t put your face too close to the soldering site because of the danger of stray hot solder and those horrible fumes.
Instead, use a magnifying device to see when soldering teeny-tiny components to a board.
You can buy clampon magnifiers that keep your hands free for soldering.
STATIC DISCHARGE PROTECTION FOR ELECTRONIC DEVICES TUTORIALS
HOW TO PROTECT ELECTRONIC DEVICES FROM ELECTROSTATIC DISCHARGE?
Protecting Electronic Components from Dreaded Static Discharge
You’re not the only thing in your work area that could suffer from shocks. Static discharge (also referred to as electrostatic discharge; ESD) can do damage to your delicate electrical components.
Static discharge is so named because it’s caused by the discharge of electrons from a static charge that hang around in an insulating body, even after the source of those electrons goes away.
Static charge is typically caused by friction. You might trap some electrons in your body as you walk across a carpet, for example. When a static charge is built up on your body, a corresponding voltage difference is built up between your body and a grounded object, such as a doorknob. The zap when you then touch a doorknob is the static discharge: that is, the electrons flowing from you to the doorknob.
What static discharge can do?
Metal oxide semiconductor (MOS) devices are cool because they allow integrated components to use less power. MOS devices improve circuit design and operation, but that improvement comes at a price. These little guys are VERY sensitive to ESD. One little zap, and they are likely to be history.
When you walk across a carpet, you can produce a static charge in the range of 2,000–4,000V. Because the number of electrons trapped on your body is low, you feel only a little shock. However, MOS devices contain a very thin layer of insulating glass that can become toast when exposed to as little as 50V of discharge or less.
When you work with a MOS device, your body, clothes, and tools have to be free of static discharge. MOS devices are found in many integrated circuits (ICs) and transistors.
ICs and transistors that use bipolar devices do not have the very thin layers of insulating glass found in MOS devices, so they are less susceptible to damage from static discharge. Resistors, capacitors, diodes, transformers, and coils, on the other hand, aren’t in too much danger from static discharge. Keep static discharge away from your projects just to be safe.
How to guard against ESD?
To get rid of static discharge in your electronics workshop, you can do several things, such as wearing anti-static devices and clothing, using static dissipative floor mats, and grounding your tools.
First, wear an anti-static wrist strap. An anti-static wrist strap is one of the best ways to get rid of ESD. You then attach the wire on the strap to earth ground — which is just what it sounds like: namely, the earth beneath your feet. The cold water pipe on a water heater or under a sink is a good option for earth ground — if the water pipes are metal, that is.
Plastic water pipes that you find in some newer construction won’t work. Because the cold water pipe comes up out of the ground, it is therefore grounded (logical, huh?), which works where the hot water pipe usually won’t. Use a clamp to attach a wire to the pipe (earth ground) and run it to your worktable, being sure to run the wire along the wall so you don’t trip over it.
Set a loop of the wire at the edge of your worktable where it’s handy to attach the alligator clip on the end of it to your wrist strap. If you don’t happen to have a metal cold water pipe nearby, the best method is to use a metal rod that you insert into the ground. The standard rule is to sink it three feet deep.
Second, wear clothing that is less likely to accumulate static charge. For example, polyester, acetate, and wool fabrics easily accumulate static charges whereas as cotton is less likely to accumulate the static charges necessary for ESD. Using an anti-static wrist strap and wearing cotton clothing will usually be sufficient.
Third, if you plan to do electronics projects long-term, consider buying a static-dissipative mat for your work surface. You connect the mat to a ground, as you do with the wrist strap, and the mat dissipates charges from components you’re working on as you lay them on the mat.
However, the mat has a high enough resistance that it won’t short together the pins of components. There are also static-dissipative floor mats; however, these are more likely to be used in a manufacturing setting when a worker needs to move between workstations.
AUTOMATIC BATHROOM LIGHT BASIC ELECTRONICS PROJECT
HOW TO MAKE AUTOMATIC BATHROOM LIGHT
This circuit is used to automate the working of a bathroom light. It is designed for a bathroom fitted with an automatic door-closer, where the manual verification of light status is difficult. The circuit also indicates whether the bathroom is occupied or not.
The circuit uses only two ICs and can be operated from a 5V supply. As it does not use any mechanical contacts it gives a reliable performance.
One infrared LED (D1) and one infrared detector diode (D2) form the sensor part of the circuit. Both the infrared LED and the detector diode are fitted on the frame of the door with a small separation between them as shown in Fig. 1. The radiation from IR LED is blocked by a small opaque strip (fitted on the door) when the door is closed.
Detector diode D2 has a resistance in the range of meg-ohms when it is not activated by IR rays. When the door is opened, the strip moves along with it. Radiation from the IR LED turns on the IR detector diode and the voltage across it drops to a low level.
C o m p a r a t o LM358 IC2(a) compares the voltage across the photodetec- tor against a reference potential set by preset VR1. The preset is so adjusted as to provide an optimum threshold voltage so that output of IC2(a) is high when the door is closed and low when the door is open.
Capacitor C1 is connected at the output to filter out unwanted transitions in output voltage generated at the time of opening or closing of the door. Thus, at point A, a low-to-high going voltage transition is available for every closing of the door after opening it. (See waveform A in Fig. 2.)
The second comparator IC2(b) does the reverse of IC2(a), as the input terminals are reversed. At point B, a low level is available when the door is closed and it switches to a high level when the door is opened. (See waveform B in Fig. 2.) Thus, a lowto- high going voltage transition\ is available at point B for every opening of the door, from the closed position.
Capacitor C2 is connected at the output to filter out unwanted transitions in the output voltage generated at the time of closing or opening of the door. IC 7474, a rising-edge-sensitive dual-D flip-flop, is used in the circuit to memorise the occupancy status of the bathroom. IC1(a) memorises the state of the door and acts as an occupancy indicator while IC2(b) is used to control the relay to turn on and turn off the bathroom light. Q output pin 8 of IC1(b) is tied to D input pin 2 of IC1(a) whereas Q output pin 5 of IC1(a) is tied to D input pin 12 of IC1(b).
At the time of switching on power for the first time, the resistor-capacitor combination R3-C3 clears the two flip-flops. As a result Q outputs of both IC1(a) and IC1(b) are low, and the low level at the output of IC1(b) activates a relay to turn on the bathroom light. This operation is independent of the door status (open/closed). The occupancy indicator red LED (D3) is off at this point of time, indicating that the
room is vacant.
When a person enters the bathroom, the door is opened and closed, which provides clock signals for IC1(b) (first) and IC1(a). The low level at point C (pin 5) isclocked in by IC1(b), at the time of opening the door, keeping the light status unchanged.
The high level point D (pin 8) is clocked in by IC1(a), turning on the occupancy indicator LED (D3) on at the time of closing of the door. (See waveform C in Fig. 2.)
When the person exits the bathroom, the door is opened again. The output of IC1(b) switches to high level, turning off the bathroom light. (See waveform D in\ Fig. 2.) The closing of the door by the door-closer produces a low-to-high transition at the clock input (pin 3) of IC1(a). This clocks in the low level at Q output of IC1(b) point D to Q output of IC1(a) point C, thereby turning off the occupancy indicator.
PRINCIPLES OF OSCILLATION BASIC AND TUTORIALS
HOW PRINCIPLES OF OSCILLATION WORKS?
A small signal voltage amplifier is shown in Fig. 1.3. In Fig. 1.3(a) the operational amplifier has no external components connected to it and the signal is fed in as shown. The operational amplifier has an extremely high gain under these circumstances and this leads to saturation within the amplifier.
As saturation implies working in the non-linear section of the characteristics, harmonics are produced and a ringing pattern may appear inside the chip. As a result of this, a square wave output is produced for a sinusoidal input. The amplifier has ceased to amplify and we say it has become unstable.
There are many reasons why an amplifier may become unstable, such as temperature changes or power supply variations, but in this case the problem is the very high gain of the operational amplifier.
Figure 1.3(b) shows how this may be overcome by introducing a feedback network between the output and the input. When feedback is applied to an amplifier the overall gain can be reduced and controlled so that the operational amplifier can function as a linear amplifier.
Note also that the signal fedback has a phase angle, due to the inverting input, which is in opposition to the input signal (Vi).
Negative feedback can therefore be defined as the process whereby a part of the output voltage of an amplifier is fed to the input with a phase angle that opposes the input signal. Negative feedback is used in amplifier circuits in order to give stability and reduced gain.
Bandwidth is generally increased, noise reduced and input and output resistances altered. These are all desirable parameters for an amplifier, but if the feedback is overdone then the amplifier becomes unstable and will produce a ringing effect.
In order to understand stability, instability and its causes must be considered. From the above discussion, as long as the feedback is negative the amplifier is stable, but when the signal feedback is in phase with the input signal then positive feedback exists.
Hence positive feedback occurs when the total phase shift through the operational amplifier (opamp) and the feedback network is 360° (0°). The feedback signal is now in phase with the input signal (Vi) and oscillations take place.
TOP VIDEO GAMES COMPANY IN THE WORLD
A RUN DOWN ON THE TOP VIDEO GAMES MAKER IN THE WORLD
Microsoft Corporation
While relatively new to the market, Microsoft has a number of products in the home consumer space including its Xbox gaming platform. Xbox hardware is built with an impressive Intel processor, a custom-designed Microsoft graphics processor with Nvidia memory, and a hard disk drive. It supports HDTV and includes a DVD, four I/O ports for the game controller, and an Ethernet port.
Nintendo
Based in Japan, Nintendo was the original developer of the Nintendo 64 and the more recent Nintendo GameCube systems. The company has stated that it is not pursuing a home gateway strategy and that it will stick to games only.
Sega
Based in Japan, Sega brought to market the Dreamcast, a second-generation 128-bit gaming console
with:
■ CD player
■ Built-in 56K modem for Internet play
■ Internet access and e-mail
■ Expansion slots for home networking.
Although Sega has exited the market to concentrate on gaming software, it was first to market with its second-generation game console. The company also provides accessories such as a keyboard, extra memory, and various controllers.
After Sega ceased production of the Dreamcast gaming console, the company refashioned itself as a platform-agnostic game developer. By the end of the year Sega will bring its games to handheld devices (such as PDAs and cell phones), set-top boxes, and even rival consoles.
In addition Sega agreed to deliver Dreamcast chip technology to set-top box manufacturers to enable cable subscribers to play Dreamcast games. Sega has been the number three video game console supplier and has been hemorrhaging money since the introduction of Dreamcast in 1999. The release of Microsoft’s Xbox most likely influenced Sega’s move to exit the game console market.
Sony
Based in Japan, Sony Computer Entertainment Inc. is positioning itself as the consumer’s one-stop shop for home consumer devices ranging from entertainment to personal computing. Sony has overcome a number of challenges to create a unified network of consumer devices and digital services.
It brought together diverse parts of the company to work together on a single, cohesive Internet strategy. Sony is positioning its 128-bit PlayStation2 as a gateway into the home from which it can offer Internet access, value-added services, and home networking.
Its home networking would use USB or iLink (also called IEEE 1394 or FireWire) ports to connect devices. PlayStation2 contains a DVD player that could enable digital video playback and could, in time, include an integrated digital video recorder. With its added functionality the Playstation2 is leaving the “game console” designation behind.
BINARY SYSTEM BASICS AND TUTORIALS
WHAT IS BINARY NUMBER SYSTEM? A TUTORIAL ON BINARY NUMBER SYSTEM
The binary number system is a radix-2 number system with ‘0’ and ‘1’ as the two independent digits. All larger binary numbers are represented in terms of ‘0’ and ‘1’. The procedure for writing higher order binary numbers after ‘1’ is similar to the one explained in the case of the decimal number system.
For example, the first 16 numbers in the binary number system would be 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110 and 1111. The next number after 1111 is 10000, which is the lowest binary number with five digits.
This also proves the point made earlier that a maximum of only 16 (= 24 numbers could be written with four digits. Starting from the binary point, the place values of different digits in a mixed binary number are 20, 21, 22 and so on (for the integer part) and 2−1, 2−2, 2−3 and so on (for the fractional part).
Example 1.1
Consider an arbitrary number system with the independent digits as 0, 1 and X. What is the radix of this number system? List the first 10 numbers in this number system.
Solution
• The radix of the proposed number system is 3.
• The first 10 numbers in this number system would be 0, 1, X, 10, 11, 1X, X0, X1, XX and 100.
Advantages
Logic operations are the backbone of any digital computer, although solving a problem on computer could involve an arithmetic operation too. The introduction of the mathematics of logic by George Boole laid the foundation for the modern digital computer.
He reduced the mathematics of logic to a binary notation of ‘0’ and ‘1’. As the mathematics of logic was well established and had proved itself to be quite useful in solving all kinds of logical problem, and also as the mathematics of logic (also known as Boolean algebra) had been reduced to a binary notation, the binary number system had a clear edge over other number systems for use in computer systems.
Yet another significant advantage of this number system was that all kinds of data could be conveniently represented in terms of 0s and 1s. Also, basic electronic devices used for hardware implementation could be conveniently and efficiently operated in two distinctly different modes.
For example, a bipolar transistor could be operated either in cut-off or in saturation very efficiently.
Lastly, the circuits required for performing arithmetic operations such as addition, subtraction, multiplication, division, etc., become a simple affair when the data involved are represented in the form of 0s and 1s.
THE 7400-SERIES DISCRETE LOGIC FAMILY IC BASICS AND TUTORIALS
WHAT IS THE 7400-SERIES DISCRETE LOGIC FAMILY INTEGRATED CIRCUITS?
With the advent of ICs in the early 1960s, engineers needed ready access to a library of basic logic gates so that these gates could be wired together on circuit boards and turned into useful products. Rather than having to design a custom microchip for each new project, semiconductor companies began to recognize a market for standard, off-the-shelf logic ICs.
In 1963 and 1964, Sylvania and Texas Instruments began shipment of the 7400-series discrete logic family and unknowingly started a de facto industry standard that lasts to this day and shows no signs of disappearing anytime soon.
Using the 7400 family, an engineer can select logic gates, flip-flops, counters, and buffers in individual packages and wire them together as desired to solve a specific problem. Some of the most common members of the 7400 family are listed in Table 2.1.
TABLE 2.1 Common 7400 ICs
Part Number Function Number of Pins
7400 Quad two-input NAND gates 14
7402 Quad two-input NOR gates 14
7404 Hex inverters 14
7408 Quad two-input AND gates 14
7432 Quad two-input OR gates 14
7447 BCD to seven-segment display decoder/driver 16
7474 Dual D-type positive edge triggered flip-flops 14
7490 Four-bit decade counter 14
74138 Three-to-eight decoder 16
74153 Dual 4-to-1 multiplexer 16
74157 Quad 2-to-1 multiplexers 16
74160 Four-bit binary synchronous counter 16
74164 Eight-bit parallel out serial shift registers 16
74174 Quad D-type flip-flops with complementary outputs 16
74193 Four-bit synchronous up/down binary counter 16
74245 Octal bus transceivers with tri-state outputs 20
74373 Octal D-type transparent latch 20
74374 Octal D-type flip-flops 20
These are just a few of the full set of 7400 family members. Many 7400 parts are no longer used, because their specific function is rarely required as a separate chip in modern digital electronics designs.
However, the parts listed above, and many others that are not listed, are still readily available today and are commonly found in a broad range of digital designs ranging from low-end to hightech devices. 7400-series logic has been available in DIPs for a long time, as well as (more recently) SOICs and other high-density surface mount packages.
All flavors of basic logic gates are available with varying numbers of inputs. For example, there are 2-, 3-, and 4-input AND gates and 2-, 3-, 4-,8-, 12-, and 13-input NAND gates. There are numerous varieties of flip-flops, counters, multiplexers, shift registers, and bus transceivers.
Flip-flops exist with and without complementary outputs, preset/ clear inputs, and independent clocks. Counters are available in 4-bit blocks that can both increment and decrement and count to either 15 (binary counter) or 9 (decade counter) before restarting the count at 0.
Shift registers exist in all permutations of serial and parallel inputs and outputs. Bus transceivers in 4- and 8 bit increments exist with different types of output enables and capabilities to function in unidirectional or bidirectional modes. Bus transceivers enable the creation and expansion of tri-state buses on which multiple devices can communicate.
One interesting IC is the 7447 seven-segment display driver. This component allows the creation of graphical numeric displays in applications such as counters and timers. Seven-segment displays are commonly seen in automobiles, microwave ovens, watches, and consumer electronics.
Seven independent on/off elements can represent all ten digits.. The 7447 is able to drive an LED-based seven-segment display when given a binary coded decimal (BCD) input. BCD is a four-bit binary number that has valid values from 0 through 9.
Hexadecimal values from 0xA through 0xF are not considered legal BCD values. Familiarity with the 7400 series proves very useful no matter what type of digital system you are designing.
For low-end systems, 7400-series logic may be the only type of IC at your disposal to solve a wide range of problems. At the high end, many people are often surprised to see a small 14- pin 7400-series IC soldered to a circuit board alongside a fancy 32-bit microprocessor running at 100 MHz.
The fact is that the basic logic functions that the 7400 series offers are staples that have direct applications at all levels of digital systems design. It is time well spent to become familiar with the extensive capabilities of the simple yet powerful 7400 family.
Manufacturers’ logic data books, either in print or on line, are invaluable references. It can be difficult to know ahead of time if a design may call for one more gate to function properly; that is when a 40-year old logic family can save the day.
BOOLEAN LOGIC ALGEBRA AND LOGIC GATES BASICS AND TUTORIAL
BOOLEAN LOGIC AND LOGIC GATES TUTORIALS
Machines of all types, including computers, are designed to perform specific tasks in exact well defined manners. Some machine components are purely physical in nature, because their composition and behavior are strictly regulated by chemical, thermodynamic, and physical properties.
For example, an engine is designed to transform the energy released by the combustion of gasoline and oxygen into rotating a crankshaft. Other machine components are algorithmic in nature, because their designs primarily follow constraints necessary to implement a set of logical functions as defined by human beings rather than the laws of physics.
A traffic light’s behavior is predominantly defined by human beings rather than by natural physical laws. This book is concerned with the design of digital systems that are suited to the algorithmic requirements of their particular range of applications. Digital logic and arithmetic are critical building blocks in constructing such systems.
An algorithm is a procedure for solving a problem through a series of finite and specific steps. It can be represented as a set of mathematical formulas, lists of sequential operations, or any combination thereof. Each of these finite steps can be represented by a Boolean logic equation.
Boolean logic is a branch of mathematics that was discovered in the nineteenth century by an English mathematician named George Boole. The basic theory is that logical relationships can be modeled by algebraic equations.
Rather than using arithmetic operations such as addition and subtraction, Boolean algebra employs logical operations including AND, OR, and NOT. Boolean variables have two enumerated values: true and false, represented numerically as 1 and 0, respectively. The AND operation is mathematically defined as the product of two Boolean values, denoted A and B for reference.
Truth tables are often used to illustrate logical relationships as shown for the AND operation in Table 1.1. A truth table provides a direct mapping between the possible inputs and outputs.
A basic AND operation has two inputs with four possible combinations, because each input can be either 1 or 0 — true or false. Mathematical rules apply to Boolean algebra, resulting in a nonzero product only when both inputs are 1.
Summation is represented by the OR operation in Boolean algebra as shown in Table 1.2. Only one combination of inputs to the OR operation result in a zero sum: 0 + 0 = 0.
Boolean variables may not seem too interesting on their own. It is what they can be made to represent that leads to useful constructs. A rather contrived example can be made from the following logical statement:
“If today is Saturday or Sunday and it is warm, then put on shorts.”
Three Boolean inputs can be inferred from this statement: Saturday, Sunday, and warm. One Boolean output can be inferred: shorts. These four variables can be assembled into a single logic equation that computes the desired result, shorts = (Saturday OR Sunday) AND warm
While this is a simple example, it is representative of the fact that any logical relationship can be expressed algebraically with products and sums by combining the basic logic functions AND, OR, and NOT.
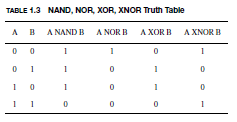
Several other logic functions are regarded as elemental, even though they can be broken down into AND, OR, and NOT functions. These are not–AND (NAND), not–OR (NOR), exclusive–OR (XOR), and exclusive–NOR (XNOR).
Table 1.3 presents the logical definitions of these other basic functions. XOR is an interesting function, because it implements a sum that is distinct from OR by taking into account that 1 + 1 does not equal 1. As will be seen later, XOR plays a key role in arithmetic for this reason.
All binary operators can be chained together to implement a wide function of any number of inputs. For example, the truth table for a ten-input AND function would result in a 1 output only when all inputs are 1.
Similarly, the truth table for a seven-input OR function would result in a 1 output if any of the seven inputs are 1. A four-input XOR, however, will only result in a 1 output if there are an odd number of ones at the inputs.
This is because of the logical daisy chaining of multiple binary XOR operations. As shown in Table 1.3, an even number of 1s presented to an XOR function cancel each other out.
It quickly grows unwieldy to write out the names of logical operators. Concise algebraic expressions are written by using the graphical representations shown in Table 1.4.
Note that each operation has multiple symbolic representations. The choice of representation is a matter of style when handwritten and is predetermined when programming a computer by the syntactical requirements of each computer programming language.
A common means of representing the output of a generic logical function is with the variable Y. Therefore, the AND function of two variables, A and B, can be written as Y = A & B or Y = A*B.
As with normal mathematical notation, products can also be written by placing terms right next to each other, such as Y = AB. Notation for the inverted functions, NAND, NOR, and XNOR, is achieved by inverting the base function.
Two equally valid ways of representing NAND are Y = A & B and Y = !(AB). Similarly, an XNOR might be written as Y = BAR A⊕BAR B.
When logical functions are converted into circuits, graphical representations of the seven basic operators are commonly used. In circuit terminology, the logical operators are called gates . Figure 1.1 shows how the basic logic gates are drawn on a circuit diagram.
Naming the inputs of each gate A and B and the output Y is for reference only; any name can be chosen for convenience. A small bubble is drawn at a gate’s output to indicate a logical inversion.
More complex Boolean functions are created by combining Boolean operators in the same way that arithmetic operators are combined in normal mathematics. Parentheses are useful to explicitly convey precedence information so that there is no ambiguity over how two variables should be
treated.
A Boolean function might be written as Y = (AB + C + )D& BAR E ⊕ BAR F
This same equation could be represented graphically in a circuit diagram, also called a schematic diagram , as shown in Fig. 1.2. This representation uses only two-input logic gates. As already mentioned, binary operators can be chained together to implement functions of more than two variables.
An alternative graphical representation would use a three-input OR gate by collapsing the two-input OR gates into a single entity.
CLOCK SKEW BASICS AND TUTORIALS
WHAT IS CLOCK SKEW? HOW CLOCK SKEW WORKS?
The preceding timing analysis example is simplified for ease of presentation by assuming that the source and destination flops in a logic path are driven by the same clock signal. Although a synchronous circuit uses a common clock for all flops, there are small, nonzero variances in clock timing at individual flops.
Wiring delay variances are one source of this nonideal behavior. When a clock source drives two flops, the two wires that connect to each flop’s clock input are usually not identical in length. This length inequality causes one flop’s clock to arrive slightly before or after the other flop’s clock.
Clock skew is the term used to characterize differences in edge timing between multiple clock inputs. Skew caused by wiring delay variance can be effectively minimized by designing a circuit so that clock distribution wires are matched in length.
A more troublesome source of clock skew arises when there are too many clock loads to be driven by a single source. Multiple clock drivers are necessary in these situations, with small variations in electrical characteristics between each driver.
These driver variances result in clock skew across all the flops in a synchronous design. As might be expected, clock skew usually reduces the frequency at which a synchronous circuit can operate.
Clock skew is subtracted from the nominal clock period for setup time analysis purposes, because the worst-case scenario shown in Fig. 1.17 must be considered. This scenario uses the same logic circuit in Fig. 1.16 but shows two separate clocks with 1 ns of skew between them.
The worst timing occurs when the destination flop’s clock arrives before that of the source flop, thereby reducing the amount of time available for the D-input to stabilize. Instead of the circuit having zero margin with a 20-ns period, clock skew increases the minimum period to 21 ns.
The extra 1 ns compensates for the clock skew to restore a minimum source to destination period time of 20 ns. A slower circuit such as this one is not very sensitive to clock skew, especially after backing off to 40 MHz for timing margin as shown previously.
Digital systems that run at relatively low frequencies may not be affected by clock skew, because they often have substantial margins built into their timing analyses. As clock speeds increase, the margin decreases to the point at which clock skew and interconnect delay become important limiting factors in system design.
Hold time compliance can become more difficult in the presence of clock skew. The basic problem occurs when clock skew reduces the source flop’s apparent tCO from the destination flop’s perspective, causing the destination’s input to change before tH is satisfied.
Such problems are more prone in high-speed systems, but slower systems are not immune. Figure 1.18 shows a timing diagram for a circuit with 1 ns of clock skew where two flops are connected by a short wire with nearly zero propagation delay.
The flops have tCO = 2 ns and tH = 1.5 ns. A scenario like this may be experienced when connecting two chips that are next to each other on a circuit board. In the absence of clock skew, the destination flop’s input would change tCO after the rising clock edge, exceeding tH by 0.5 ns.
The worst-case clock skew causes the source flop clock to arrive before that of the destination flop, resulting in an input change just 1 ns after the rising clock edge and violating tH. Solutions to skew-induced tH violations include reducing the skew or increasing the delay between source and destination.
Unfortunately, increasing a signal’s propagation delay may cause tSU violations in high-speed systems. Hold time may not be a problem in slower circuits, because slower circuits often have paths between flops with sufficiently long propagation delays to offset clock skew problems.
However, even slow circuits can experience hold-time problems if flops are connected with wires or components that have small propagation delays. It is also important to remember that hold-time compliance is not a function of clock period but of clock skew, tCO, and tH. Therefore, a slow system that uses fast components may have problems if the clock skew exceeds the difference between tCO and tH.
OPERATIONAL AMPLIFIER BASICS AND TUTORIALS
WHAT IS AN OPERATIONAL AMPLIFIER?
An operational amplifier or op amp is a circuit that takes an input voltage and amplifies it. The symbol used to represent an op amp in a circuit diagram is shown in Fig. 9-1.
An op amp is defined by two simple equations. The first thing to note is that the voltage across the input terminals is zero. Hence Va = Vb
The second relation that is essential for analyzing op amp circuits is that the currents drawn at a and b in Fig. 9-1 are zero Ia = Ib = 0
Despite this, we will see that the op amp will result in voltage gains at the output terminal c. How does this work? Two voltages are input to terminals a and b.
Their difference is then amplified and output at c, which is taken with referenc to ground. Although we won’t worry about the internal construction of an op amp, note that it consists of a set of resistors and dependent voltage source. The internal voltage source is related to the input voltages by A(V+ − V−)
The constant A is known as the open-loop voltage gain. To see how op amp circuits work, it’s best to examine some popular example circuits.
When analyzing op amp circuits, remember to take the input voltage across the op amp terminals to be zero and that the op amp draws zero current. The analysis is then reduced to applying KVL and KCL to the circuit elements connected to the op amp.
SOLDERING IRON BASIC INFORMATION AND TUTORIALS
WHAT IS SOLDERING IRON? HOW TO USE SOLDERING IRON?
 |
| SOLDERING IRON |
Soldering is used in nearly every phase of electronic construction so you’ll need soldering tools. A soldering tool must be hot enough to do the job and lightweight enough for agility and comfort.
A temperature controlled iron works well, although the cost is not justified for occasional projects. Get an iron with a small conical or chisel tip.
Soldering is not like gluing; solder does more than bind metal together and provide an electrically conductive path between them. Soldered metals and the solder combine to form an alloy.
You may need an assortment of soldering irons to do a wide variety of soldering tasks. They range in size from a small 25-watt iron for delicate printed-circuit work to larger 100 to 300-watt sizes used to solder large surfaces.
If you could only afford a single soldering tool when initially setting up your electronics workbench than, an inexpensive to moderately priced pencil-type soldering iron with between 25 and 40-watt capacity is the best for PC board electronics work.
A 100-watt soldering gun is overkill for printed-circuit work, since it often gets too hot, cooking solder into a brittle mess or damaging small parts of a circuit. Soldering guns are best used for point-to-point soldering jobs, for large mass soldering joints or large components.
Small “pencil” butane torches are also available, with optional soldering-iron tips. Butane soldering irons are
ideal for field service problems and will allow you to solder where there is no 110 volt power source.
Keep soldering tools in good condition by keeping the tips well tinned with solder. Do not run them at full
temperature for long periods when not in use. After each period of use, remove the tip and clean off any scale that may have accumulated.
Clean an oxidized tip by dipping the hot tip in sal ammoniac (ammonium chloride) and then wiping it clean with a rag. Sal ammoniac is somewhat corrosive, so if you don’t wipe the tip thoroughly, it can contaminate electronic soldering.
Place the tip of the soldering iron into the “Tip Tinner” after every few solder joints. If a copper tip becomes pitted, file it smooth and bright and then tin it immediately with solder.
Modern soldering iron tips are nickel or iron clad and should not be filed. The secret of good soldering is to use the right amount of heat.
Many people who will have not soldered before use too little heat dabbing at the joint to be soldered and making little solder blobs that cause unintended short circuits.
Always use caution when soldering. A hot soldering iron can burn your hand badly or ruin a tabletop. It’s a good idea to buy or make a soldering iron holder.
COLPITTS OSCILLATORS BASIC CIRCUIT TUTORIALS
WHAT ARE COLPITTS OSCILLATORS?
Colpitts oscillators are similar to the shunt fed Hartley oscillator circuit except the Colpitts oscillator, instead of having a tapped inductor, utilizes two series capacitors in its LC circuit.
With the Colpitts oscillator the connection between these two capacitors is used as the center tap for the circuit. A Colpitts oscillator circuit is shown at Figure 2-5, and you will see some similarities with the Hartley oscillator.
 |
| Colpitts Oscillators |
The simplest Colpitts oscillator to construct and get running is the “series tuned” version, more often referred to as the “Clapp Oscillator.” Because there is no load on the inductor, a high “Q” circuit results with a high L/C ratio and of course much less circulating current.
This aids drift reduction. Because larger inductances are required, stray inductances do not have as much impact as perhaps in other circuits.
The total capacitive reactance of the parallel combination of capacitors depicted as series tuning below the inductor in a series tuned Colpitts oscillator or “Clapp oscillator” should have a total reactance of around 200 ohms.
Not all capacitors may be required in your particular application. Effectively all the capacitors are in series in a Colpitts oscillator, i.e. they appear as parallel connected but their actual values are in fact in series.
Ideally, your frequency determining components L1 and the parallel capacitors should be in a grounded metal shield. The FET used in the Colpitts oscillator is the readily available 2N4416A.
Note, the metal FET case is connected to the circuit ground. The output from the Colpitts oscillator is through output capacitor 47 pF; this should be the smallest of values possible, consistent with continued reliable operation into the next buffer amplifier stage.
555 TIMER BASICS AND TUTORIALS
WHAT IS 555 TIME AND HOW 555 TIMER WORKS?
Creating a Pulse
The 555 is made out of simple transistors that are about the same as on / off switches. They do not have any sense of time. When you apply a voltage they turn on and when you take away the voltage they turn off. So by itself, the 555 can not create a pulse.
The way the pulse is created is by using some components in a circuit attached to the 555 (see the circuit on the next page). This circuit is made of a capacitor and a resistor. We can flip a switch and start charging the capacitor.
The resistor is used to control how fast the capacitor charges. The bigger the resistance, the longer it takes to charge the capacitor.
The voltage in the capacitor can then be used as an input to another switch. Since the voltage starts at 0, nothing happens to the second switch. But eventually the capacitor will charge up to some
point where the second switch comes on. The way the 555 timer works is that when you flip the first switch, the Output pin goes to Vcc (the positive power supply voltage) and starts charging the capacitor.
When the capacitor voltage gets to 2/3 Vcc (that is Vcc * 2/3) the second switch turns on which makes the output go to 0 volts.
The pinout for the 555 timer is shown below:
Pin 2 (Trigger) is the 'on' switch for the pulse. The line over the word Trigger tells us that the voltage levels are the opposite of what you would normally expect. To turn the switch on you apply 0 volts to pin 2.
The technical term for this opposite behavior is 'Active Low'. It is common to see this 'Active Low' behavior for IC inputs because of the inverting nature of transistor circuits.
Pin 6 is the off switch for the pulse. We connect the positive side of the capacitor to this pin and the negative side of the capacitor to ground. When Pin 2 (Trigger) is at Vcc, the 555 holds Pin 7 at 0 volts (Note the inverted voltage).
When Pin 2 goes to 0 volts, the 555 stops holding Pin 7 at 0 volts. Then the capacitor starts charging. The capacitor is charged through a resistor connected to Vcc. The current starts flowing into the capacitor, and the voltage in the capacitor starts to increase.
Pin 3 is the output (where the actual pulse comes out). The voltage on this pin starts at 0 volts. When 0 volts is applied to the trigger (Pin 2), the 555 puts out Vcc on Pin 3 and holds it at Vcc until
Pin 6 reaches 2/3 of Vcc (that is Vcc * 2/3). Then the 555 pulls the voltage at Pin 3 to ground and you have created a pulse. (Again notice the inverting action.) The voltage on Pin 7 is also pulled to ground, connecting the capacitor to ground and discharging it.
Seeing the pulse
To see the pulse we will use an LED connected to the 555 output, Pin 3. When the output is 0 volts the LED will be off. When the output is Vcc the LED will be on.
Place the 555 across the middle line of the breadboard so that 4 pins are on one side and 4 pins are on the other side. (You may need to bend the pins in a little so they will go in the holes.)
Leave the power disconnected until you finish building the circuit. The diagram above shows how the pins on the 555 are numbered. You can find pin 1 by looking for the half circle in the end of the chip. Sometimes instead of a half circle, there will be a dot or shallow hole by pin 1.
Before you start building the circuit, use jumper wires to connect the red and blue power rows to the red and blue power rows on the other side of the board. Then you will be able to easily reach Vcc and Ground lines from both sides of the board. (If the wires are too short, use two wires joined together in a row of holes for the positive power (Vcc) and two wires joined together in a different row of holes for the ground.)
Connect Pin 1 to ground.
Connect Pin 8 to Vcc.
Connect Pin 4 to Vcc.
Connect the positive leg of the LED to a 330 ohm resistor and connect the negative end of the
LED to ground. Connect the other leg of the 330 ohm resistor to the output, Pin 3.
Connect Pin 7 to Vcc with a 10k resistor (RA = 10K).
Connect Pin 7 to Pin 6 with a jumper wire.
Connect Pin 6 to the positive leg of the 220uF Capacitor (C = 220uF). (You will need to bend the positive (long leg) up and out some so that the negative leg can go in the breadboard.
Connect the negative leg of the capacitor to ground.
Connect a wire to Pin 2 to use as the trigger. Start with Pin 2 connected to Vcc.
Now connect the power. The LED will come on and stay on for about 2 seconds. Remove the wire connected to Pin 2 from Vcc. You should be able to trigger the 555 again by touching the wire connected to pin 2 with your finger or by connecting it to ground and removing it. (It should be about a 2 second pulse.)
Making it Oscillate
Next we will make the LED flash continually without having to trigger it. We will hook up the 555 so that it triggers itself. The way this works is that we add in a resistor between the capacitor and the discharge pin, Pin 7.
Now, the capacitor will charge up (through RA and RB) and when it reaches 2/3 Vcc, Pin 3 and Pin 7 will go to ground. But the capacitor can not discharge immediately because of RB. It takes some time for the charge to drain through RB.
The more resistance RB has, the longer it takes to discharge. The time it takes to discharge the capacitor will be the time the LED is off.
To trigger the 555 again, we connect Pin 6 to the trigger (Pin 2). As the capacitor is discharging, the voltage in the capacitor gets lower and lower.
When it gets down to 1/3 Vcc this triggers Pin 2 causing Pin 3 to go to Vcc and the LED to come on. The 555 disconnects Pin 7 from ground, and the capacitor starts to charge up again through RA and RB.
To build this circuit from the previous circuit, do the following.
Disconnect the power.
Take out the jumper wire between Pin 6 and Pin 7 and replace it with a 2.2k resistor (RB =2.2K).
Use the jumper wire at pin 2 to connect Pin 2 to Pin 6.
Now reconnect the power and the LED should flash forever (as long as you pay your electricity bill).
Experiment with different resistor values of RA and RB to see how it changes the length of time that the LED flashes. (You are changing the amount of time that it takes for the Capacitor to charge and discharge.)
Formulas
These are the formulas we use for the 555 to control the length of the pulses.
t1 = charge time (how long the LED is on) = 0.693 * (RA + RB) * C
t2 = discharge time (how long the LED is off) = 0.693 * RB * C
T = period = t1 + t2 = 0.693 * (RA + 2*RB) * C
Frequency = 1 / T = 1.44 / ((RA + 2 * RB) * C)
t1 and t2 are the time in seconds. C is the capacitor value in Farads. 220uF = 0.000220 F. So
for our circuit we have:
t1 = 0.693 * (10000 + 2200) * 0.000220 = 1.86 seconds
t2 = 0.693 * 2200 * 0.000220 = 0.335 seconds
T = 1.86 + 0.335 = 2.195 seconds
Frequency = 0.456 (cycles per second)
LASER CONTROLLED ON OFF SWITCH USING 555 TIMER BASIC ELECTRONICS PROJECT
HOW TO MAKE LASER CONTROLLED ON OFF SWITCH?
This is a basic electronic project on how to make a laser controlled on/ off switch using a 555 timer. Below is its schematic diagram.
This circuit is built around a 555 timer using very few components. Since the circuit is very simple, even a novice can easily build it and use it as a controlling device.
A laser pointer, now easily available in the market, can be used to operate this device. This circuit has been tested in operational conditions from a distance of 500 metres and was found to work satisfactorily though it can be controlled from still longer distances.
Aiming (aligning) the laser beam exactly on to the LDR is a practical problem. The circuit is very useful in switching on/off a fan at night without getting off the bed. It can also be used for controlling a variety of other devices like radio or music system.
The limitation is that the circuit is operational only in dark or dull-lit environments. By focussing the laser beam on LDR1 the connected gadget can be activated through the relay, whereas by focussing laser beam on LDR2 we can switch off the gadget.
The timer is configured to operate in bistable mode.
TOUCH ACTIVATED ALARM SYSTEM BASIC ELECTRONIC PROJECT
TOUCH ACTIVATED ALARM SYSTEM PROJECT USING 555 TIMER
This is a basic electronic project of Touch Activate Alarm System using a 555 timer. The 555 can be a LM, NE, or MC(cmos) type, they are all pin-compatible. **C1/C2's working voltage should be increased to 25V if you decide to go with a 12V power source. Below is the schematic diagram.
Parts List
R1 = 100K
D1 = 1N4004
U1 = 555 Timer*
R2 = 56K
C1 = 47μF/16V**
R3 = 10M
C2 = 33μF/16V**
R4 = 220K
T1 = 2N3904, or equivalent
P1 = 100K
Re1 = Relay***
Rule of thumb: the working voltage of capacitors are at least double the supplied voltage, in other words, if the powersource is 9Volt, your capacitor(s) is at least 18V. Transistor T1 can be any approximate substitute. *** Use any suitable relay for your project and if you're not tight on space, use any size. I've build this particular circuit to prevent students from fiddling with the security cameras in computer labs at the
University I am employed. I made sure the metal casing was not grounded. But as the schematic shows you can basically hook it up to any type of metal surface. I used a 12-vdc power source. Use any suitable relay to handle your requirements.
A 'RESET' switch (Normally Closed) can be added between the positive and the 'arrow-with-the-+'. The trigger (touch) wire is connected to pin 2 of the 555 and will trigger the relay, using your body resistance, when touched. It is obvious that the 'touching' part has to be clean and makes good contact with the trigger wire.
This particular circuit may not be suitable for all applications. Just in case you wonder why pin 5 is not listed in the schematic diagram; it is not really needed. In certain noisy conditions a small ceramic capacitor is placed between pin 5 and ground. It does no harm to add one or leave it out.
NOTE: For those of you who did not notice, there is an approximate 5-second delay build-in before activation of the relay to avoid false triggering, or a 'would-be' thief, etc.
AGAIN, make sure the latch is not touching anything 'ground' or the circuit just keeps resetting itself and so will not work. My shed has wooden doors so works fine. If you can not get yours to work, check the trigger input, verify there is some sort of signal coming from output pin 3 play with the value of R3.
Subscribe to:
Posts (Atom)